Book
- An Introduction to Optimization, 4th Edition - Edwin Chong and Stanislaw Zak
Complete Handwritten Notes
Intro
In this section we consider the optimization problem
minimizef(x)subjecttox∈Ω. The function f:Rn→R that we wish to minimize is a real-valued function called the objective function or cost function. The vector x is an n-vector of independent variables: x=[x1,x2,⋯,xn]T∈Rn. Tha variables x1,⋯,xn are often referred to as decision variables. The set Ω is a subset of Rn called the constraint set or feasible set.
Definition
Suppose that f:Rn→R is a real-valued function defined on some set Ω⊂Rn. A point x∗∈Ω is a local minimizer of f over Ω is there exists ε>0 such that f(x)≥f(x∗) for all x∈Ω if f(x)≥f(x∗) for all x∈Ω\{x∗}.
Conditions for Local Minimizers
Definition
A vector d∈Rn,d=0, is a feasible direction at x∈Ω if there exists α0>0 such that x+αd∈Ω for all α∈[0,α0].
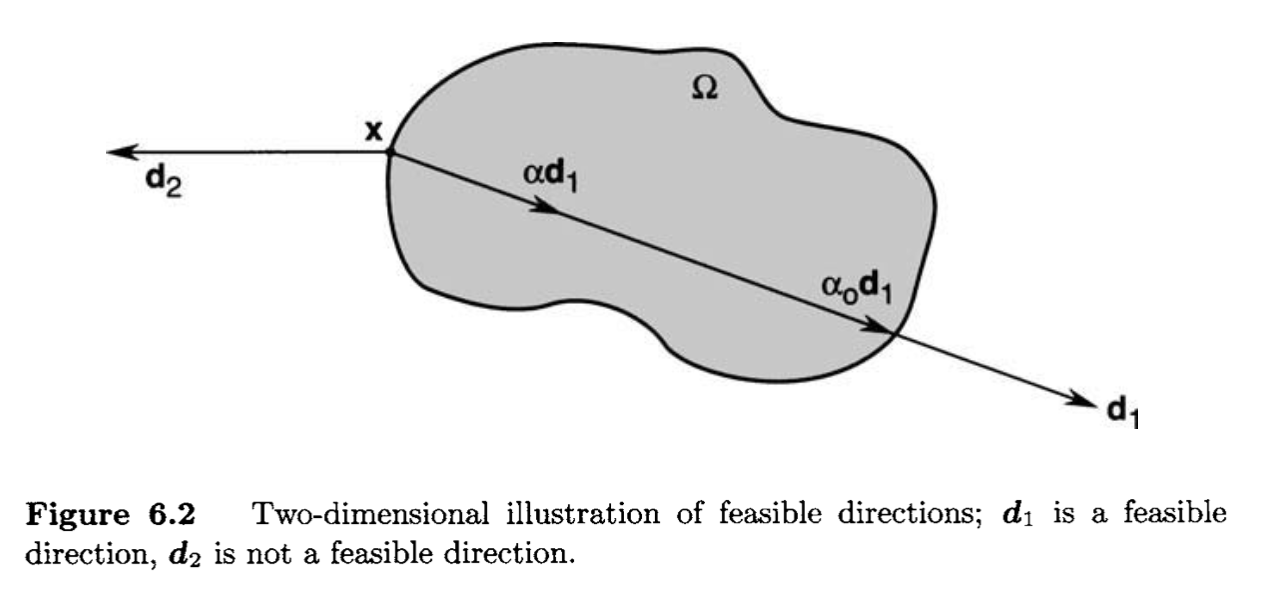
Theorem of First-Order Necessary Condition (FONC)
Let Ω be a subset of Rn and f∈C1 a real-valued function on Ω. If x∗ is a local minimizer of f over Ω, then for any feaible direction d at x∗, we have
dT∇f(x∗)≥0. Proof
Define
x(α)=x∗+αd∈Ω. Note that x(0)=x∗. Define the composite funcition
ϕ(α)=f(x(α)). Then, by Taylor's theorem,
f(x∗+αd)−f(x∗)=ϕ(α)−ϕ(0)=ϕ′(0)α+o(α)=αdT∇f(x(0))+o(α), where α≥0. Thus, if ϕ(α)≥ϕ(0), that is, f(x∗+αd)≥f(x∗) for sufficiently small values of α>0 (x∗ is a local minimizer), then we have to have dT∇f(x∗)≥0.
Corollary (Interior Case)
Let Ω be a subset of Rn and f∈C1 a real-valued function on Ω. If x∗ is a local minimizer of f over Ω and if X∗ is an interior point of Ω, then
∇f(x∗)=0. Proof
Suppose that f has a local minimizer x∗ that is an interior point of Ω. Because x∗ is an interior point of Ω, the set of feasible dierctions at x∗ is the whole of Rn. This, for any d∈Rn, which implies that ∇f(x∗)=0.
Theorem of Second-Order Necessary Condition (SONC)
Let Ω⊂Rn,f∈C2 a function on Ω,x∗ a local minimizer of f over Ω, and d a feasible direction at x∗. If dT∇f(x∗)=0, then
dTF(x∗)d≥0, where F is the Hessian of f.
Proof
We prove the result by contradiction. Suppose that there is a feasible direction d at x∗ such that dT∇f(x∗)=0 and dTF(x∗)d<0. Let x(α)=x∗+αd and define the composite function ϕ(α)=f(x∗+αd)=f(x(α)). Then, by Taylor's theorem,
ϕ(α)=ϕ(0)+ϕ′′(0)2α2+o(α2), where by assumption, ϕ′(0)=dT∇f(x∗)=0 and ϕ′′(0)=dTF(x∗)d<0. For sufficiently small α,
ϕ(α)−ϕ(0)=ϕ′′(0)2α2+o(α2)<0, that is,
f(x∗+αd)<f(x∗), which contradicts the assumption that x∗ is a local minimizer. Thus,
ϕ′′(0)=dTF(x∗)d≥0. Corollary (Interior Case)
Let x∗ be an interior point of Ω⊂Rn. If x∗ is a local minimizer of f:Ω→R,f∈C2, then
∇f(x∗)=0, and F(x∗) is positive semidefinite (F(x∗)≥0); that is, for all d∈Rn,
dTF(x∗)d≥0. Proof
If x∗ is an interior point, then all directions are feasible. The result then follows from the previous corollary and SONC.
Theorem of Second-Order Sufficient Condition (SOSC), Interior Case
Let f∈C2 be defined on a region in which x∗ is an interior point. Suppose that
- ∇f(x∗)=0.
- F(x∗)>0.
Then, x∗ is a strict local minimizer of f.
Proof
Because f∈C2, we have F(x∗)=FT(x∗). Using assumption 2 and Rayleigh's inequality it follows that if d=0, then 0<λmin(F(x∗))∥d∥2≤dTF(x∗)d. By Taylor's theorem and assumption 1,
f(x∗+d)−f(x∗)=21dTF(x∗)d+o(∥d∥2)≥2λmin(F(x∗))∥d∥2+o(∥d∥2). Hence, for all d such that ∥d∥ is sufficiently small,
f(x∗+d)>f(x∗), which completes the proof.
